■ 역행렬
실수계에서 $a$가 $0$이 아닌 실수라면 $ab = ba = 1$인 실수 $b$가 존재, $b$를 $a$의 곱셈역원(multiplicative inverse)이라하고 $a^{-1}$로 표시
$A$를 $n \times n$ 행렬이라 하자. $AB = BA = I$ 인 행렬 $B$가 존재한다면, 행렬 $A$를 정칙 또는 가역행렬이라 한다. 행렬 $B$를 $A$의 역행렬이라 한다.
ex) $A = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}$, $B = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix}$ $B=a^{-1}$
$AB = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} = \begin{bmatrix} 2 \times 1 + 1 \times 1 & 2 \times (-1) + 1 \times 2 \\ 1 \times 1 + 1 \times 1 & 1 \times (-1) + 1 \times 2 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
※ 실수계 : 0이 아닌 모든 실수는 곱셈역원을 갖는다.
행렬 : 0행렬이 아닌 모든 $n \times n$행렬 $A$가 역행렬을 갖는것이 아니다.
ex) $A = \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix}$, $B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}$
$AB = \begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} b_{11} + b_{21} & b_{12} + b_{22} \\ 0 & 0 \end{bmatrix}$
특이행렬 : 역행렬을 갖지 않는 행렬
역행렬의 성질, $A$와 $B$가 정칙 행렬
1) $(A^{-1} )^{1} = A$
2) $(AB)^{-1} = B^{-1} A^{-1}$
3) $(A^{T} )^{-1} = (A^{-1} )^{T}$
■ 수반행렬(adjoint matrix)
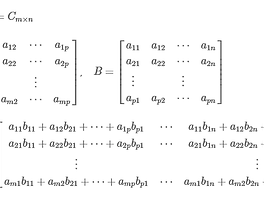
$A$를 $n \times n$ 행렬이라고 하자. $A$의 원소에 대응하는 여인수로 된 전치행렬을 $A$의 수반행렬이라고 하고 $\text{adj} A$로 표기한다.
$\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & \cdots & C_{2n} \\ \vdots &&& \vdots \\ C_{n1} & C_{n2} & \cdots & C_{nn} \end{bmatrix}^{T} =\begin{bmatrix} C_{11} & C_{21} & \cdots & C_{n1} \\ C_{12} & C_{22} & \cdots & C_{n2} \\ \vdots &&& \vdots \\ C_{1n} & C_{2n} & \cdots & C_{nn} \end{bmatrix}$
■ 역행렬 구하기
$A$가 $n \times n$ 행렬, $A \neq 0$ ($n \ge 4$ 적용하기 어려움)
$A^{-1} = \left ( \frac{1}{\text{det} A} \right ) \text{adj} A$
$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$, 여인수 $C_{11} = a_{22}$, $C_{12} = -a_{21}$, $C_{21} = -a_{12}$, $C_{22} = a_{11}$
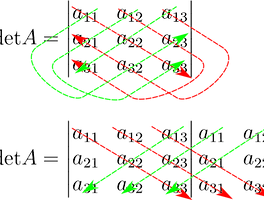
$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$, $C_{11} = \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}$, $C_{12} = -\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix}$, $C_{13} = \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}$
$A^{-1} = \frac{1}{\text{det} A} \begin{bmatrix} C_{11} & C_{21} & C_{31} \\ C_{12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \end{bmatrix}$
ex) $2 \times 2$ 행렬
$A = \begin{bmatrix} 1 & 4 \\ 2 & 10\end{bmatrix}$, $A^{-1} = \frac{1}{\text{det} A} (\text{adj} A)$
$\text{det} A = (10 -8) = 2$
$\text{adj} A = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22}\end{bmatrix}^{T} = \begin{bmatrix} 10 & -2 \\ -4 & 1 \end{bmatrix}^{T} = \begin{bmatrix} 10 & -4 \\ -2 & 1\end{bmatrix}$
∴ $A^{T} = \frac{1}{2} \begin{bmatrix} 10 & -4 \\ -2 & 1 \end{bmatrix} = \begin{bmatrix} 5 & -2 \\ -1 & 1/2\end{bmatrix}$
검산
$AA^{-1} = \begin{bmatrix} 1 & 4 \\ 2 & 10 \end{bmatrix} \begin{bmatrix} 5 & -2 \\ -1 & 1/2 \end{bmatrix} = \begin{bmatrix} 5-4 & -2+2 \\ 10-10 & -4+5 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
$A^{-1} A = \begin{bmatrix} 5 & -2 \\ -1 & 1/2 \end{bmatrix} \begin{bmatrix} 1 & 4 \\ 2 & 10 \end{bmatrix} = \begin{bmatrix} 5-4 & 20-20 \\ -1+1 & -4+5 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
ex) $3 \times 3$ 행렬
$A = \begin{bmatrix} 2 & 2 & 0 \\ -2 & 1 & 1 \\ 3 & 0 & 1 \end{bmatrix}$, $A^{-1} = \frac{1}{\text{det} A} (\text{adj} A)$
$\text{det} A = 2(-1)^{1+1} \begin{vmatrix} 1 & 1 \\ 0 & 1 \end{vmatrix} + 2(-1)^{1+2} \begin{vmatrix} -2 & 1 \\ 3 & 1\end{vmatrix}$
$= 2 \times 1 + (-2)(-2-3) = 2 +10 = 12$
$\text{adj} A = \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix}^{T}$
$C_{11} = \begin{vmatrix} 1 & 1 \\ 0 & 1\end{vmatrix} =1$, $C_{12} = -\begin{vmatrix} -2 & 1 \\ 3 & 1\end{vmatrix} =5$, $C_{13} = \begin{vmatrix} -2 & 1 \\ 3 & 0 \end{vmatrix} =-3$
$C_{21} = -\begin{vmatrix} 2 & 0 \\ 0 & 1\end{vmatrix} =-2$, $C_{22} = \begin{vmatrix} 2 & 0\\ 3 & 1\end{vmatrix} =2$, $C_{23} = -\begin{vmatrix} 2 & 2 \\ 3 & 0\end{vmatrix} =6$
$C_{31} = \begin{vmatrix} 2 & 0 \\ 1 & 1\end{vmatrix} =2$, $C_{32} = \begin{vmatrix} 2 & 0 \\ -2 & 1\end{vmatrix} =2$, $C_{33} = \begin{vmatrix} 2 & 2 \\ -2 & 1\end{vmatrix} =6$
$\text{det} A = \begin{vmatrix} 1 & 5 & -3 \\ -2 & 2 & 6 \\ 2 & -2 & 6 \end{vmatrix}^{T} = \begin{vmatrix} 1 & -2 & 2\\ 5 & 2 & -2 \\ -3 & 6 & 6 \end{vmatrix}$
∴ $A^{-1} = \frac{1}{12} \begin{vmatrix} 1 & -2 & 2\\ 5 & 2 & -2 \\ -3 & 6 & 6 \end{vmatrix} = \begin{vmatrix} 1/12 & -1/6 & 1/6 \\ 5/12 & 1/6 & -1/6 \\ -1/4 & 1/2 & 1/2 \end{vmatrix}$
※ 역행렬의 존재성
$A$가 $n \times n$ 행렬일때, $A^{-1}$이 존재할 필요 충분 조건은 $\text{rank} A = n$이고, 따라서 $\text{det} A \neq 0$이다. 따라서 $\text{rank} A = n$이면, $A$는 정치행렬이고 $\text{rank} A < n$이면 특이행렬이다.
'Study materials > Mathematics' 카테고리의 다른 글
| 행렬(Matrix) 9. 역행렬을 이용한 연립방정식 풀이 (1) | 2021.03.31 |
|---|---|
| 행렬(Matrix) 8. Gauss-Jordan 소거법(행 연산법) (0) | 2021.03.30 |
| 행렬(Matrix) 6. Cramer 법칙 (0) | 2021.03.29 |
| 행렬(Matrix) 5. 행렬식의 성질 (0) | 2021.03.29 |
| 행렬(Matrix) 4. 행렬식 (0) | 2021.03.25 |