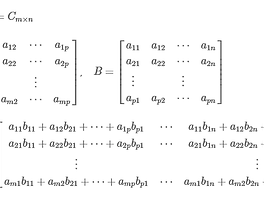
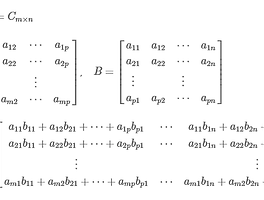
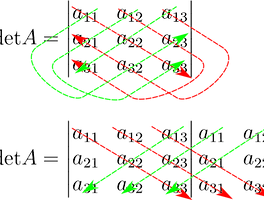
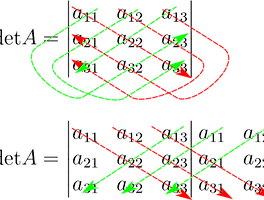
■ Cramer 법칙
$\begin{matrix} a_{11} x_{1} + a_{12} x_{2} + \cdots + a_{1n} x_{n} = b_{1} \\ a_{21} x_{1} + a_{22} x_{2} + \cdots + a_{2n} x_{n} = b_{2} \\ \vdots \\ a_{n1} x_{1}+ a_{n2} x_{2} + \cdots + a_{nn} x_{n} = b_{n} \end{matrix}$
$\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & & \cdots& \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{bmatrix}$ $\text{det} A \neq 0$ 단일해
$x_{j} = \frac{\begin{vmatrix} a_{11} & a_{12} & \cdots & b_{1} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & b_{2} & \cdots & a_{2n} \\ \vdots &&&& \vdots \\a_{n1} & a_{n2} & \cdots & b_{n} & \cdots & a_{nn} \end{vmatrix} } {\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1j} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} & \cdots & a_{2n} \\ \vdots &&&& \vdots \\a_{31} & a_{32} & \cdots & a_{3j} & \cdots & a_{3n} \end{vmatrix} }$ $\begin{matrix}= D_{1} = \text{det} A^{'} (1 \leq j \leq n) \\ \\= D = \text{det} A \end{matrix} $
$x_{1} = \frac{D_{1}}{D} = \frac{\text{det} A_{1}}{\text{det} A}$, $x_{2} = \frac{D_{2}}{D} = \frac{\text{det} A_{2}}{\text{det} A}$, $x_{n} = \frac{D_{n}}{D} = \frac{\text{det} A_{n}}{\text{det} A}$
ex) Cramer 법칙을 이용하여 연립방정식 풀이
$\begin{matrix} 3 x_{1} + 2 x_{2} + x_{3} = 7 \\ x_{1} + x_{2} + 3 x_{3} = 3 \\ 5x_{1} + 4x_{2} - 2x_{3} = 1\end{matrix}$ $\Rightarrow$ $\begin{bmatrix} 3 & 2 & 1 \\ 1 &-1 & 3 \\ 5 & 4 &-2 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} 7 \\ 3 \\ 1 \end{bmatrix}$
$A$
$\text{det} A = 3(-1)^{1+1} \begin{vmatrix} -1 & 3 \\ 4 & -2\end{vmatrix} + 2(-1)^{1+2} \begin{vmatrix} 1 & 3 \\ 5 & -2\end{vmatrix} + 1(-1)^{1+3} \begin{vmatrix} 1 & -1 \\ 5 & 4\end{vmatrix}$
$= 3(2-12) + (-2)(-2-15) + 1(4+5) = -30+34+9 = 13$
$\text{det} A_{1} = \begin{vmatrix} 7 & 2 & 1 \\ 3 & -1 & 3 \\ 1 & 4 & -2 \end{vmatrix}$
$= 7(-1)^{1+1} \begin{vmatrix} -1 & 3 \\ 4 & -2 \end{vmatrix} + 2(-1)^{1+2} \begin{vmatrix} 3 & 3 \\ 1 & -2 \end{vmatrix} + 1(-1)^{1+3} \begin{vmatrix} 3 & -1 \\ 1 & 4 \end{vmatrix}$
$= 7(2-12) + (-2)(-6-3) + 1(12+1) = -70 +18 + 13 = -39$
$= 3(2-12) + (-2)(-2-15) + 1(4+5) = -30+34+9 = 13$
$\text{det} A_{2} = \begin{vmatrix} 3 & 7 & 1 \\ 1 & 3 & 3 \\ 5 & 1 & -2 \end{vmatrix}$
$= 3(-1)^{1+1} \begin{vmatrix} 3 & 3 \\ 1 & -2 \end{vmatrix} + 7(-1)^{1+2} \begin{vmatrix} 1 & 3 \\ 5 & -2 \end{vmatrix} + 1(-1)^{1+3} \begin{vmatrix} 1 & 3 \\ 5 & 1 \end{vmatrix}$
$= 3(-6-3) + (-7)(-2-15) + 1(1-15) = -27 +119 - 14 = 78$
$\text{det} A_{3} = \begin{vmatrix} 3 & 2 & 7 \\ 1 & -1 & 3 \\ 5 & 4 & 1 \end{vmatrix}$
$= 3(-1)^{1+1} \begin{vmatrix} -1 & 3 \\ 4 & 1 \end{vmatrix} + 2(-1)^{1+2} \begin{vmatrix} 1 & 3 \\ 5 & 1 \end{vmatrix} + 7(-1)^{1+3} \begin{vmatrix} 1 & -1 \\ 5 & 4 \end{vmatrix}$
$= 3(-1-12) + (-2)(1-15) + 7(4+5) = -39 +28 +63 = 52$
∴ $x_{1} = \frac{\text{det} A_{1}}{\text{det} A} = \frac{-39}{13} = -3$, $x_{2} = \frac{\text{det} A_{2}}{\text{det} A} = \frac{78}{13} = 6$, $x_{3} = \frac{\text{det} A_{3}}{\text{det} A} = \frac{52}{13} = 4$
'Study materials > Mathematics' 카테고리의 다른 글
| 행렬(Matrix) 8. Gauss-Jordan 소거법(행 연산법) (0) | 2021.03.30 |
|---|---|
| 행렬(Matrix) 7. 역행렬 (0) | 2021.03.29 |
| 행렬(Matrix) 5. 행렬식의 성질 (0) | 2021.03.29 |
| 행렬(Matrix) 4. 행렬식 (0) | 2021.03.25 |
| 행렬(Matrix) 3. 선형 연립방정식(2) (0) | 2021.03.24 |