AASHTO LRFD BRIDGE DESIGN SPECIFICATION(AASHTO, 2012) SECTION 13 : RAILINGS
○ 설계하중(Design Forces)
| Design Forces and Designations | Railing Test Levels | |||||
| TL-1 | TL-2 | TL-3 | TL-4 | TL-5 | TL-6 | |
| $F_{t}$ Transverse(N) | 60,000 | 120,000 | 240,000 | 240,000 | 550,000 | 780,000 |
| $F_{L}$ Longitudinal(N) | 20,000 | 40,000 | 80,000 | 80,000 | 183,000 | 260,000 |
| $F_{v}$ Vertical(N) Down | 20,000 | 20,000 | 20,000 | 80,000 | 355,000 | 355,000 |
| $L_{t}$ and $L_{L}$ (mm) | 1,220 | 1,220 | 1,220 | 1,070 | 2,440 | 2,440 |
| $L_{v}$ (mm) | 5,500 | 5,500 | 5,500 | 5,500 | 12,200 | 12,200 |
| $H_{e}$ (min)(mm) | 460 | 510 | 610 | 810 | 1,070 | 1,420 |
| Minimum $H$ Height of Rail(mm) | 685 | 685 | 685 | 810 | 1,070 | 2,290 |
○ 강도 평가
항복선 이론에 의한 저항능력(Load-Carrying Capacity)
콘크리트 방호벽의 저항능력은 철근콘크리트의 항복선 이론(Yield Line Theory)에 의하여 구할 수 있다. 즉, 그림 1과 같이 파괴면을 따라 소성힌지가 형성된다는 가정 하에 외력과 내력에 의해 행해진 일의 합은 영(0)이 된다는 조건으로부터 콘크리트 방호벽의 저항하중과 파괴길이를 구하는 것이다.
분포하중($F_{t}$)에 의한 외적인 일
콘크리트 방호벽의 강도를 알기위해 개발된 이 식은 극한 상태에서 항복선의 형성에 기초를 두고 있다. 차량하중은 $L_{t}$에 걸쳐 분포되는 하중 $F_{t}$를 발생시키며, 그 차량 충돌에 의해 일어나는 항복선 형태는 그림 1과 같이 가정할 수 있다. 필수적으로 벽이나 슬래브의 기하학적 조건과 경계조건이 일치하는 하나의 항복선 형태에 대해 작용하중으로 인한 외적 일과 항복선에 따른 저항 모멘트에 의해 행해진 내적 일을 같게 둠으로써(가상일의 원리) 하나의 해가 얻어진다. 경사진 항복선의 각은 임계길이 $L_{c}$에 의해 표현될 수 있으므로 외적일과 내적일은 모두 $L_{c}$의 함수가 되고 가상일의 원리로부터 $F_{t}$를 $L_{c}$의 함수($F_{t} (L_{t} )$)로 나타낼 수 있게 된다. 작용하중 $F_{t}$는 이러한 상한의 해 중에서 최소값을 의미하므로 이를 구하기 위해 $F_{t} (L_{t} )$를 $L_{c}$에 대하여 최소화하여 구할 수 있다.

작용하중에 의한 외적 일은 다음과 같다.
그림 1의 벽 상단에 나타난 변형전과 변형후의 위치는 그림 2에 나타나있다. 빗금 친 부분의 면적은 등분포하중($W_{t} = F_{t} / L_{t} $)이 작용하는데 따른 변형의 합을 나타낸다.
가상변위 $\delta$ 에 대하여, 변위 $x$ 는 식 1과 같다.
$x = \frac{L_{c} - L_{t}}{L_{c}}$ (식 1)

또한, 빗금 친 부분의 면적은 식 2와 같다.
$A = \frac{1}{2} (\delta + x) L_{t} = \frac{\delta}{2} (1+ \frac{L_{c} - L_{t}}{L_{c}}) L_{t}$
$= \delta \frac{L_{t}}{L_{c}} (\frac{L_{c}}{2} + \frac{L_{c} - L_{t}}{2}) = \delta \frac{L_{t}}{L_{c}} (L_{c} - \frac{L_{t}}{2} )$ (식 2)
그러므로, 등분포하중 $W_{t}$에 의해 행해진 외적일 $W$ 는 식 3과 같다
$W = W_{t} \times A = \frac{F_{t}}{L_{t}} [\delta \frac{L_{t}}{L_{c}} (L_{c} - \frac{L_{t}}{2})]$
$= F_{t} \times \delta \frac{(L_{c} - \frac{L_{t}}{2})} {L_{c}}$
항복선에 따른 내적인 일
항복선에 따른 내적일은 이일이 작용하는데 따른 항복 모멘트와 회전의 곱에 의한 합계이다. 조각난 벽체들은 회전이 모두 항복선에 집중되기 위해 강체인 것으로 가정된다.
그림 3과 같이 벽의 상단에서 작은 변형에 대해 조각난 벽체의 회전 $\theta$ 는 식 4와 같다.
$\theta = tan \theta = \frac{2\delta}{L_{c}}$ (식 4)

콘크리트 방호벽은 상단의 보와 아래의 균등한 두께의 벽으로 구분하여 해석 될 수 있다. 극한 상태에서 상단의 보 공칭 휨모멘트 $M_{n}$과 같은 소성모멘트 $M_{b}$를 발생시킨다. 정·부 소성모멘트 강도가 같다고 가정하면, 상단보에 의해 행해진 내적일 $U_{b}$는 식 5와 같다.
$U_{b} = 4 M_{b} \theta = \frac{8 M_{b} \delta}{L_{c}}$ (식 5)
콘크리트 방호벽의 벽부분은 통상적으로 수평과 수직의 두 방향으로 철근이 배근될 것이다. 벽에서의 수평철근은 수직축에 대하여 단위길이당 저항모멘트 $M_{w}$를 일으킨다. 벽에서의 수직철근은 수평축에 대하여 단위길이당 캔틸레버 저항모멘트 $M_{c}$ 를 일으킨다. 이러한 두 모멘트 성분은 그림 4에 나타낸 것처럼 경사진 항복선에 대하여 저항모멘트 $M_{a}$를 일으킨다. 경사진 항복선에 따른 내적 일을 결정할 때 수직 및 수평축에 대한 모멘트의 투영과 회전을 사용하는 것이 더 간단하다.
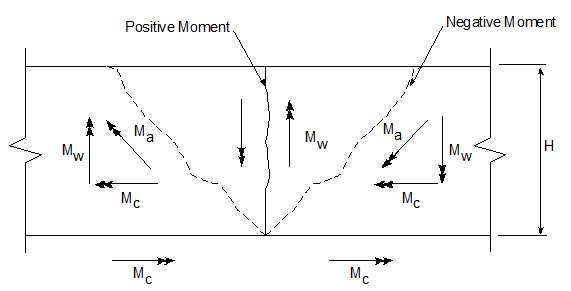
그림 4와 같이 수직축에 대한 정·부 모멘트 $M_{w}$가 같다고 하면, 벽 모멘트 $M_{w} H$에 의해 행해진 내적일 $U_{w}$는 식 6과 같다.
$U_{w} = 4 M_{w} H \theta = \frac{8 M_{w} H \delta}{L_{c}}$ (식 6)
콘크리트 방호벽의 캔틸레버 작용에 의한 경사각은 $\delta / H$ 이고 캔틸레버 모멘트 $M_{c} L_{c}$에 의해 행해진 내적 일 $U_{w}$는 식 7과 같다.
$U_{c} = M_{c} L_{c} \theta = \frac{M_{c} L_{c} \delta}{H}$ (식 7)
앞에서 살펴본 외적일 $W$와 내적일 $U$를 같게 두면, 외적일은 차량충돌로 발생되는 콘크리트 방호벽의 변형으로 인하여 생기는 일이며, 내적일은 보 거동을 하는 콘크리트 방호벽 상단의 저항모멘트에 의한 일이라고 할 수 있다.
$U_{b}$와 콘크리트 방호벽 벽체의 단위 높이 당 저항모멘트에 의한 일 $U_{w}$와 콘크리트 방호벽의 캔틸레버 거동에 의한 단위길이당 저항모멘트에 의하여 발생되는 일 $U_{c}$ 의 합 ($W = U_{b} + U_{w} + U_{c} $)에 앞에서 구한 식 3, 식 5, 식 6 및 식 7을 대입하면 식 8과 같다.
$\frac{F_{t} (L_{c} - \frac{L_{t}}{2}) \delta }{L_{c}} = \frac{8 M_{b} \delta}{L_{c}} + \frac{8 M_{w} \delta}{L_{c}} + \frac{M_{c} L_{c} \delta}{H}$ (식 8)
위 식을 에 관하여 풀면, 식 9와 같다.
$F_{t} ( L_{c} - \frac{L_{t}}{2} ) \delta = 8 M_{b} + 8 M_{w} H \delta + \frac{M_{c} L_{c}^{2}}{H}$
$F_{t} = \frac{8 M_{b}}{(L_{c} - \frac{L_{t}}{2})} + \frac{8 M_{w} H}{(L_{c} - \frac{L_{t}}{2})} + \frac{M_{c} L_{c}^{2}}{H(L_{c} - \frac{L_{t}}{2})}$ (식 9)
이 식은 벽에서의 부모멘트 항복선에 대한 기울기를 결정하는 임계 길이 $L_{c}$ 에 의해 좌우된다. $F_{t}$를 최소화하는 $L_{c}$에 대하여 미분한 결과가 영(0)과 같다고 둠으로써 결정될 수 있다.
즉, 식 10과 같다.
$\frac{dF_{t}}{dL_{c}} = 0$
$L_{c} = \frac{L_{t}}{2} + \sqrt{{(\frac{L_{t}}{2})^{2}} + \frac{8H(M_{b} + M_{w} H)}{M_{c}}}$ (식 10)
이 값을 식 9에 대입하여 $F_{t}$의 최소값이 나오게 되며, 그 결과는 $R_{w}$로 나타내어진다.
$min F_{t} = R_{w}$
여기서, $R_{w}$ 는 횡 하중에 대한 공칭 콘크리트 방호벽의 저항력이다. 정리하면 식 11과 같이 쓸 수 있다.
$R_{w} = \frac{2}{2 L_{c} - L_{t}} (8 M_{b} + 8 M_{w} H + \frac{M_{c} L_{c}^{2}}{H})$ (식 11)
이상을 정리하면 차량 충돌 시 콘크리트 방호벽이 파괴되는 임계 길이 $L_{c}$는 식 12와 같다.
$L_{c} = \frac{L_{t}}{2} + \sqrt{(\frac{L_{t}}{2})^{2} + \frac{8 H(M_{b} + M_{w} H)}{M_{c}}} $ (식 12)
따라서, 콘크리트 방호벽의 저항능력 $R_{w}$는 식 13과 같다.
$R_{w} = \frac{2}{2 L_{c} - L_{t}} (8 M_{b} + 8 M_{w} H + \frac{M_{c} L_{c}^{2}}{H})$ (식 13)
여기서,
$H$ : 콘크리트 방호벽의 높이
$L_{c}$ : 콘크리트 방호벽의 파괴길이
$L_{t}$ : 충돌하중의 재하길이
$M_{b}$ : 보 거동을 하는 콘크리트 방호벽 상단의 저항모멘트
$M_{w}$ : 콘크리트 방호벽 벽체의 단위 높이 당 저항모멘트
$M_{c}$ : 콘크리트 방호벽과 교량 바닥판간의 캔틸레버 거동에 의한 단위 길이 당 저항모멘트
'References(자료실) > Standard & Guide(관련 기준)' 카테고리의 다른 글
| 노측용 차량방호울타리(가드레일) 설치 기준 높이 관련 기준(해외) (0) | 2021.02.16 |
|---|---|
| 차량 충돌하중 산정 : 가속도-시간 모델 (0) | 2021.02.15 |
| SAE J211-1 SURFACE VEHICLE RECOMMENDED PRACTICE (0) | 2021.01.26 |
| Estimating Occupant Risk Without Vehicle Acceleration Data (0) | 2021.01.26 |
| 차량방호안전시설 기준 개정 역사(국내/미국) (0) | 2021.01.25 |



