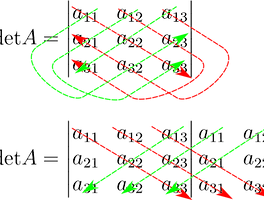
■ 행렬식 : 백터 미적분에서 부피 계산에 사용, 연립방정식 풀이에 사용
행렬 $A$ 를 $m \times n$ 행렬이라고 할때
$\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix}$ $\text{det}A = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{vmatrix}$
$m \times n$ 행렬의 행렬식을 $n$ 계의 행렬식이라 한다.
$1 \times 1$ 행렬 :
$A = [a]$, $\text{det} A = \begin{vmatrix} a \end{vmatrix} = a$
ex) $A = [-5]$, $\text{det} A = \begin{vmatrix} -5 \end{vmatrix} = -5$
$2 \times 2$ 행렬 :
$A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix}$, $\text{det} A = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12} a_{21}$
ex) $A = \begin{bmatrix} 6 & -3 \\ 5 & 9 \end{bmatrix}$, $\text{det} A = \begin{vmatrix} 6 & -3 \\ 5 & 9 \end{vmatrix} =(6 \times 9) - (-3 \times 5) = 69$
$3\times3$ 행렬 :
$A = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$, $\text{det} A = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}$
$\text{det} A = a_{11} a_{22} a_{23} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{12} a_{31} - a_{12} a_{21} a_{33} - a_{11} a_{32} a_{23}$
인수분해하여 나타내면
$\text{det} A = a_{11} (a_{22} a_{23} - a_{23} a_{32}) + a_{12} (-a_{21} a_{33} + a_{23} a_{31}) + a_{13} (a_{21} a_{32} - a_{22} a_{31})$ → ( )안은 $2 \times 2$ 행렬식

여인수(여인자), 보조인자, cofactor
$\text{det} A = a_{11} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} + a_{12} \left ( -\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix}\right ) + a_{13} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}$
$\text{det} A$ 는 $a_{11}$, $a_{12}$, $a_{13}$ 의 여인수가 행렬식의 제1행에 따라서 여인수들로 전개되었다.
$C_{11} = \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}$, $C_{12} = -\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix}$, $C_{13} = \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}$
$\text{det} A = a_{11} C_{11} + a_{12} C_{12} + a_{13} C_{13}$
일반적으로 $a_{ij}$ 의 여인수는 행렬식 $C_{ij} = (-1)^{i+j} M_{ij}$
여기서, $M_{ij}$ 는 $A$의 $i$ 행과 $j$ 열을 제거한 부분행렬의 행렬식(소행렬식 이라 한다.)
$i+j$ 가 짝수 , $C_{ij} = M_{ij}$
$i+j$ 가 홀수 , $C_{ij} = -M_{ij}$
$3 \times 3$ 행렬은 9개의 여인수를 갖는다.
$C_{11} = M_{11}$ $C_{12} = -M_{12}$ $C_{13} = M_{13}$
$C_{21} = -M_{21}$ $C_{22} = M_{22}$ $C_{23} = -M_{23}$
$C_{31} = M_{31}$ $C_{32} = -M_{32}$ $C_{33} = M_{33}$
$\begin{matrix} + & + & + \\ - & + & - \\ + & - & + \end{matrix}$
인수분해를 다시하면(2열)
$\text{det} A = a_{11} a_{22} a_{23} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{22} - a_{13} a_{22} a_{31} - a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33}$
$= -a_{12} (a_{21} a_{33} - a_{23} a_{31}) + a_{22}(a_{11} a_{33} - a_{13} a_{31}) - a_{32} (a_{11} a_{23} - a_{13} a_{21})$
$= a_{12} \left ( - \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33}\end{vmatrix} \right ) + a_{22} \begin{vmatrix} a_{11} & a_{13} \\ a_{31} & a_{33}\end{vmatrix} a_{12} + \left ( - \begin{vmatrix} a_{11} & a_{13} \\ a_{21} & a_{23}\end{vmatrix} \right )$
$=a_{12} C_{12} + a_{22} C_{22} + a_{32} C_{32}$
인수분해를 3열
$\text{det} A = a_{31} C_{31} + a_{32} C_{32} + a_{33} C_{33}$
ex 1) 다음 행렬의 행렬식을 구하라
$A = \begin{bmatrix} 2 & 4 & 7 \\ 6 & 0 & 3 \\ 1 & 5 & 3\end{bmatrix}$
1행에 따라 여인수 전개
$\text{det} A = \begin{vmatrix} 2 & 4 & 7 \\ 6 & 0 & 3 \\ 1 & 5 & 3\end{vmatrix} = 2C_{11} + 4 C_{12} + 7 C_{13}$
$C_{11} = (-1)^{1+1} \begin{vmatrix} 2 & 4 & 7 \\ 6 & 0 & 3 \\ 1 & 5 & 3\end{vmatrix} = (-1)^{2} \begin{vmatrix} 0 & 3 \\ 5 & 3 \end{vmatrix}$
$C_{12} = (-1)^{1+2} \begin{vmatrix} 2 & 4 & 7 \\ 6 & 0 & 3 \\ 1 & 5 & 3\end{vmatrix} = (-1)^{3} \begin{vmatrix} 6 & 3 \\ 1 & 3 \end{vmatrix}$
$C_{13} = (-1)^{1+3} \begin{vmatrix} 2 & 4 & 7 \\ 6 & 0 & 3 \\ 1 & 5 & 3\end{vmatrix} = (-1)^{4} \begin{vmatrix} 6 & 0 \\ 1 & 5 \end{vmatrix}$
$\text{det} A = 2(-1)^{2} \begin{vmatrix} 0 & 3 \\ 5 & 3 \end{vmatrix} + 4(-1)^{3} \begin{vmatrix} 6 & 3 \\ 1 & 3 \end{vmatrix} + 7(-1)^{4} \begin{vmatrix} 6 & 0 \\ 1 & 5 \end{vmatrix}$
$= 2(0 \times 3 - 3 \times 5) - 4(6 \times 3 - 3 \times 1) + 7(6 \times 5 - 0 \times 1)$
$= -30 - 60 + 210 = 120$
2행에 따라 여인수 전개
$\text{det} A = 6C_{21} + 0C_{22} + 3C_{23}$
$= 6(-1)^{1+2} \begin{vmatrix} 4 & 7 \\ 5 & 3 \end{vmatrix} + 3(-1)^{2+3} \begin{vmatrix} 2 & 4 \\ 1 & 5 \end{vmatrix}$
$= -6(4 \times 3 - 7 \times 5 ) - 3(2 \times 5 - 4 \times 1)$
$= -6(-23) - 3(6) = 120$
ex 2)
$A = \begin{bmatrix} 6 & 5 & 0 \\ -1 & 8 & -7 \\ -2 & 4 & 0\end{bmatrix}$ 3열에 0이 2개, 이 열을 여인수로 전개
$\text{det} A = \begin{vmatrix} 6 & 5 & 0 \\ -1 & 8 & -7 \\ -2 & 4 & 0 \end{vmatrix} = 0C_{13} + (-7)C_{23} + 0 C_{33}$
$= (-7)(-1)^{2+3} \begin{vmatrix} 6 & 5 & 0 \\ -7 & 8 & -7 \\ -2 & 4 & 0\end{vmatrix} = (-7)(-1)^{5} \begin{vmatrix} 6 & 5 \\ -2 & 4\end{vmatrix}$
$= 7(6 \times 4 - 5 \times (-2)) = 238$
$4 \times 4$ 행렬 : 각 여인수는 $3 \times 3$ 부분행렬의 부호가 붙은 소행렬식
여인수에 대한 부호는 $3 \times 3$ 행렬에서 확장
$\begin{matrix} + & - & + & - \\ - & + & - & + \\ + & - & + & - \\ - & + & - & +\end{matrix}$ $\begin{matrix} + & - & + & - & + & \cdots \\ - & + & - & + & - & \cdots \\ + & - & + & - & + & \cdots \\ - & + & - & + & - & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \end{matrix}$
ex)
$A = \begin{bmatrix} 5 & 1 & 2 & 4 \\ -1 & 0 & 2 & 3 \\ 1 & 1 & 6 & 1 \\ 1 & 0 & 0 &-4 \end{bmatrix}$ 제 4행에 0이 2개 이므로 $\text{det} A$ 를 4행에 따라 여인수로 전개한다.
$\text{det} A = \begin{vmatrix} 5 & 1 & 2 & 4 \\ -1 & 0 & 2 & 3 \\ 1 & 1 & 6 & 1 \\ 1 & 0 & 0 &-4 \end{vmatrix} = 1C_{41} + 0C_{42} + 0 C_{43} + (-4)C_{44}$
여기서,
$C_{41} = (-1)^{4+1} \begin{vmatrix} 5 & 1 & 2 & 4 \\ -1 & 0 & 2 & 3 \\ 1 & 1 & 6 & 1 \\ 1 & 0 & 0 &-4 \end{vmatrix} = (-1)^{5} \begin{vmatrix} 1 & 2 & 4 \\ 0 & 2 & 3 \\ 1 & 6 & 1\end{vmatrix}$
$C_{44} = (-1)^{4+4} \begin{vmatrix} 5 & 1 & 2 & 4 \\ -1 & 0 & 2 & 3 \\ 1 & 1 & 6 & 1 \\ 1 & 0 & 0 &-4 \end{vmatrix} = (-1)^{8} \begin{vmatrix} 5 & 1 & 2 \\ -1 & 0 & 2 \\ 1 & 1 & 6\end{vmatrix}$
두 행렬식을 제2행에 따라 여인수로 전개
$C_{41} = (-1) \begin{vmatrix} 1 & 2 & 4 \\ 0 & 2 & 3 \\ 1 & 6 & 1 \end{vmatrix} $
$= (-1) \left ( 0 \times (-1)^{2+1} \begin{vmatrix} 1 & 2 & 4 \\ 0 & 2 & 3 \\ 1 & 6 & 1\end{vmatrix} \right ) + 2(-1)^{2+2} \begin{vmatrix} 1 & 2 & 4 \\ 0 & 2 & 3 \\ 1 & 6 & 1 \end{vmatrix} + 3(-1)^{2+3} \begin{vmatrix} 1 & 2 & 4 \\ 0 & 2 & 3 \\ 1 & 6 & 1 \end{vmatrix} $
$= (-1) \left [ \left ( 2 \begin{vmatrix} 1 & 4 \\ 1 & 1\end{vmatrix} \right ) + \left ( 3(-1) \begin{vmatrix} 1 & 2 \\ 1 & 6 \end{vmatrix} \right ) \right]$
$= (-1)[2 \times (1 \times 1 - 4 \times 1) + (-3)(1 \times 6 - 2 \times 1) ]$
$= (-1)[-6 + (-12)] = 18$
$C_{44} = (-1)^{4+4} \begin{vmatrix} 5 & 1 & 2 \\ -1 & 0 & 2 \\ 1 & 1 & 6 \end{vmatrix} $
$= (1) \left ( (-1) \times (-1)^{2+1} \begin{vmatrix} 1 & 2 \\ 1 & 6 \end{vmatrix} + (0)(-1)^{2+2} \begin{vmatrix} 5 & 2 \\ 1 & 6 \end{vmatrix} + (2)(-1)^{2+3} \begin{vmatrix} 5 & 1 \\ 1 & 1 \end{vmatrix} \right )$
$= 1(1 \times 6 - 2 \times 1 ) + 0 + (-2)(5 \times 1 - 1 \times 1 )$
$= 4 -8 = -4$
∴ $\text{det} A = (1)(18) + (-4)(-4) = 34 $
'Study materials > Mathematics' 카테고리의 다른 글
| 행렬(Matrix) 6. Cramer 법칙 (0) | 2021.03.29 |
|---|---|
| 행렬(Matrix) 5. 행렬식의 성질 (0) | 2021.03.29 |
| 행렬(Matrix) 3. 선형 연립방정식(2) (0) | 2021.03.24 |
| 행렬(Matrix) 3. 선형 연립방정식(1) (0) | 2021.03.23 |
| 행렬(Matrix) 2. 행렬의 연산 (0) | 2021.03.03 |