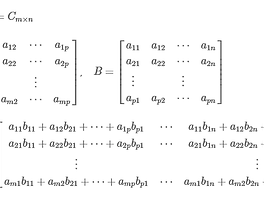
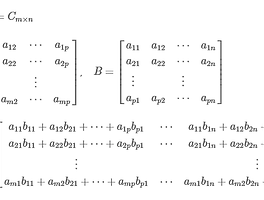
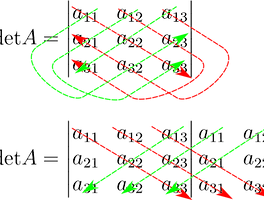
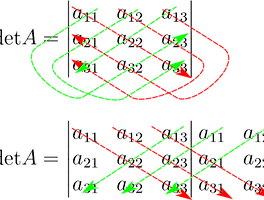
■ Cramer 법칙
a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋮an1x1+an2x2+⋯+annxn=bn
[a11a12⋯a1na21a22⋯a2n⋮⋯⋮an1an2⋯ann][x1x2⋮xn]=[b1b2⋮bn] detA≠0 단일해
xj=|a11a12⋯b1⋯a1na21a22⋯b2⋯a2n⋮⋮an1an2⋯bn⋯ann||a11a12⋯a1j⋯a1na21a22⋯a2n⋯a2n⋮⋮a31a32⋯a3j⋯a3n| =D1=detA′(1≤j≤n)=D=detA
x1=D1D=detA1detA, x2=D2D=detA2detA, xn=DnD=detAndetA
ex) Cramer 법칙을 이용하여 연립방정식 풀이
3x1+2x2+x3=7x1+x2+3x3=35x1+4x2−2x3=1 ⇒ [3211−1354−2][x1x2x3]=[731]
A
detA=3(−1)1+1|−134−2|+2(−1)1+2|135−2|+1(−1)1+3|1−154|
=3(2−12)+(−2)(−2−15)+1(4+5)=−30+34+9=13
detA1=|7213−1314−2|
=7(−1)1+1|−134−2|+2(−1)1+2|331−2|+1(−1)1+3|3−114|
=7(2−12)+(−2)(−6−3)+1(12+1)=−70+18+13=−39
=3(2−12)+(−2)(−2−15)+1(4+5)=−30+34+9=13
detA2=|37113351−2|
=3(−1)1+1|331−2|+7(−1)1+2|135−2|+1(−1)1+3|1351|
=3(−6−3)+(−7)(−2−15)+1(1−15)=−27+119−14=78
detA3=|3271−13541|
=3(−1)1+1|−1341|+2(−1)1+2|1351|+7(−1)1+3|1−154|
=3(−1−12)+(−2)(1−15)+7(4+5)=−39+28+63=52
∴ x1=detA1detA=−3913=−3, x2=detA2detA=7813=6, x3=detA3detA=5213=4
'Study materials > Mathematics' 카테고리의 다른 글
| 행렬(Matrix) 8. Gauss-Jordan 소거법(행 연산법) (0) | 2021.03.30 |
|---|---|
| 행렬(Matrix) 7. 역행렬 (0) | 2021.03.29 |
| 행렬(Matrix) 5. 행렬식의 성질 (0) | 2021.03.29 |
| 행렬(Matrix) 4. 행렬식 (0) | 2021.03.25 |
| 행렬(Matrix) 3. 선형 연립방정식(2) (0) | 2021.03.24 |