행렬(Matrix) 8. Gauss-Jordan 소거법(행 연산법)

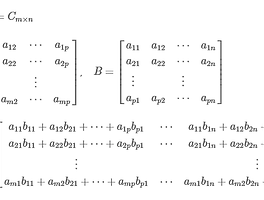
■ Gauss-Jordan 소거법

    $n \times n$ 행렬 $A$가 일련의 기본 행연산에 의하여  $n \times n$의 단위행렬 $I$로 변환, $A$는 정칙행렬

    $\begin{bmatrix} A | I \end{bmatrix} = \left [ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n}  \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots &&& \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots &&& \vdots \\ 0 & 0 & \cdots & 1 \end{matrix} \right ]$

    $\begin{bmatrix} A | I \end{bmatrix}  \Rightarrow  \begin{bmatrix} I | A^{-1} \end{bmatrix}$

 

ex 1)

    $A = \begin{bmatrix} -1 & 1 & 2 \\ 3 & -1 & 1 \\ -1 & 3 & 4 \end{bmatrix}$

가우스 소거법

    $\begin{bmatrix} A | I \end{bmatrix} = \left [ \begin{matrix} -1 & 1 & 2 \\ 3 & -1 & 1 \\ -1 & 3 & 4 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right ]$    $\begin{matrix} R_{2} + R_{1} (3) \\ R_{3} + (-1) R_{1}\end{matrix}$

         $ = \left [ \begin{matrix} -1 & 1 & 2 \\ 0 & 2 & 7 \\ 0 & 2 & 2 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ -1 & 0 & 1 \end{matrix} \right ]$    $\begin{matrix} R_{3} + (-1)R_{2} \end{matrix}$

         $ = \left [ \begin{matrix} -1 & 1 & 2 \\ 0 & 2 & 7 \\ 0 & 0 & -5 \end{matrix} \right | \left . \begin{matrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ -4 & -1 & 1 \end{matrix} \right ]$ $\begin{matrix} (-1)R_{1} \\ (0.5)R_{2} \\ (-0.2)R_{3} \end{matrix}$

        $ = \left [ \begin{matrix} 1 & -1 & -2 \\ 0 & 1 & 35 \\ 0 & 0 & 1 \end{matrix} \right | \left . \begin{matrix} -1 & 0 & 0 \\ 1.5 & 0.5 & 0 \\ 0.8 & 0.2 & -0.2 \end{matrix} \right ]$ $\begin{matrix} R_{1} +(2)R_{3} \\ R_{2} +(-3.5)R_{3} \end{matrix}$

        $ = \left [ \begin{matrix} 1 & -1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right | \left . \begin{matrix} 0.6 & 0.4 & -0.4 \\ -1.3 & -0.2 & 0.7 \\ 0.8 & 0.2 & -0.2 \end{matrix} \right ]$ $\begin{matrix} R_{1} +R_{2} \end{matrix}$

         $ = \left [ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right | \left . \begin{matrix} -0.7 & 0.2 & 0.3 \\ -1.3 & -0.2 & 0.7 \\ 0.8 & 0.2 & -0.2 \end{matrix} \right ]$

검증

       $\begin{bmatrix} -1 & 1 & 2 \\ 3 & -1 &  1 \\ -1 & 3 & 4 \end{bmatrix} \begin{bmatrix} -0.7 & 0.2 & 0.3 \\ -1.3 & -0.2 &  0.7 \\ 0.8 & 0.2 & -0.2 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 &  0 \\ 0 & 0 & 1 \end{bmatrix} $

       $(-1)(0.7) + (1)(-1.3) + (2)(0.8) = -0.7 + (-0.3) - 1.6 = 1$

        ∴ $AA^{-1} = I$    $A^{-1}A = I$

 

ex2)

    $A = \begin{bmatrix} 2 & 0 & 1 \\ -2 & 3 & 4 \\ -5 & 5 & 6 \end{bmatrix}$

        $\left [ \begin{matrix} 2 & 0 & 1 \\ -2 & 3 & 4 \\ -5 & 5 & 6 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right ]$    $\begin{matrix} 1/2R_{1} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 0.5 \\ -2 & 3 & 4 \\ -5 & 5 & 6 \end{matrix} \right |  \left . \begin{matrix} 0.5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right ]$

        $\begin{matrix} 2R_{1} + R_{2} \\ 5R_{1} + R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 1/2 \\ 0 & 3 & 5 \\ 0 & 5 & 17/2 \end{matrix} \right |  \left . \begin{matrix} 1/2 & 0 & 0 \\ 1 & 1 & 0 \\ 5/2 & 0 & 1 \end{matrix} \right ]$

        $\begin{matrix} 1/3R_{2} \\ 1/5R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 1/2 \\ 0 & 1 & 5/3 \\ 0 & 1 & 17/10 \end{matrix} \right |  \left . \begin{matrix} 1/2 & 0 & 0 \\ 1/3 & 1/3 & 0 \\ 1/2 & 0 & 1/5 \end{matrix} \right ]$

        $\begin{matrix} (-1)R_{2} + R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 1/2 \\ 0 & 1 & 5/3 \\ 0 & 0 & 1/30 \end{matrix} \right |  \left . \begin{matrix} 1/2 & 0 & 0 \\ 1/3 & 1/3 & 0 \\ 1/6 & -1/3 & 1/5 \end{matrix} \right ]$

        $\begin{matrix} 30R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 1/2 \\ 0 & 1 & 5/3 \\ 0 & 0 & 1 \end{matrix} \right |  \left . \begin{matrix} 1/2 & 0 & 0 \\ 1/3 & 1/3 & 0 \\ 5 & -10 & 6 \end{matrix} \right ]$

        $\begin{matrix} (-1/3)R_{3} + R_{1} \\ (-5/3)R_{3} +R_{2}\\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right |  \left . \begin{matrix} -2 & 5 & -3 \\ -8 & 17 & -10 \\ 5 & -10 & 6 \end{matrix} \right ]$

 

ex 3) 특이행렬

    $A = \begin{bmatrix} 1 & -1 & -2 \\ 2 & 4 & 5 \\ 6 & 0 & -3 \end{bmatrix}$

        $\left [ \begin{matrix} 2 & 0 & 1 \\ -2 & 3 & 4 \\ -5 & 5 & 61 & -1 & -2 \\ 2 & 4 & 5 \\ 6 & 0 & -3 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right ]$    $\begin{matrix} (-1)R_{1} + R_{2} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & -1 & -2 \\ 0 & 6 & 9 \\ 6 & 0 & -3 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right ]$

        $\begin{matrix} (-6)R_{1} + R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & -1 & -2 \\ 0 & 6 & 9 \\ 0 & 6 & 9 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ -6 & 0 & 1 \end{matrix} \right ]$

        $\begin{matrix} (-1)R_{2} + R_{3} \\ \Rightarrow \end{matrix}$    $\left [ \begin{matrix} 1 & -1 & -2 \\ 0 & 6 & 9 \\ 0 & 0 & 0 \end{matrix} \right |  \left . \begin{matrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ -4 & -1 & 1 \end{matrix} \right ]$    0행을 가지므로 특이행렬