행렬(Matrix) 10. 행렬의 고유값 문제

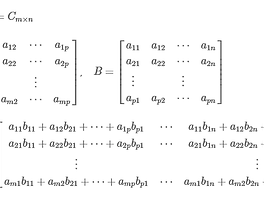
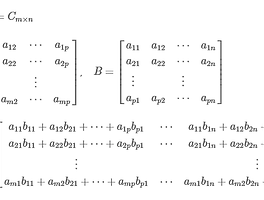
행렬이 고유값 문제는 다음 형태의 연립방정식과 관련된다.

        $Ax = \lambda x$        (1)

                $A$는 정행방렬(2×2,3×3,n×n),    $x$, $\lambda$는 구하려는 미지의 벡터, 스칼라

        $x=0$, $0=0$  $\lambda$와 관계없이 식(1)을 만족

        $\Rightarrow$ 식(1)의 $x \neq 0$인 해, 행렬 $A$의 고유 벡터

        $\Rightarrow$ $x \neq 0$인 해, 어떤 특정한 $\lambda$에 대해서만 존재, 이 값을 행렬 $A$의 고유값

식(1)을 푸는 것은 벡터 $x$에 행렬 $A$를 곱하는 것이 벡터 $x$에 스칼라 $\lambda$를 곱하는 것과 같은 영향을 갖는 $x$를 찾는 것

$\Rightarrow$ 얻어지는 스칼라 곱 $\lambda x$는 $x$의 성분에 비례하는 성분을 가지며 $\lambda$는 비례상수

 

■ 고유값, 고유벡터

        주어진 $n \times n$ 행렬 $A[a_{jk} ]$에 대하여 다음의 벡터 방정식을 고려

                $Ax = \lambda x$,        $x$ : 벡터,    $\lambda$ : 스칼라

                $\Rightarrow$ $0$벡터 : 모든 $x$의 해(실용적으로 무의미)

                      $x \neq 0$ 인 해,  $\lambda$ : 고유값, $x$ : 고유벡터

 

■ 고유값과 고유벡터 계산법

    ex 1)

        $A = \begin{bmatrix} -5 & 2 \\ 2 & -2 \end{bmatrix}$

    a) 고유값 : 우선적으로 결정되어야 한다.

        $Ax = \begin{bmatrix} -5 & 2 \\ 2 & -2 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \lambda \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}$

        성분별로 풀어쓰면

                $-5x_{1} + 2x_{2} = \lambda x_{1}$

                $2x_{1} - 2x_{2} = \lambda x_{2}$

        우변을 좌변으로 옮기면

                $(-5-\lambda ) x_{1} + 2 x_{2} = 0$        (2*)

                $2x_{1} + (-2-\lambda) x_{2} = 0$

        행렬 표기

                $\left ( \begin{bmatrix} -5-\lambda & 2 \\ 2 & -2-\lambda \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}\right ) \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$

                $(A- \lambda I) x = 0$

                Crammer 정리에 의해 자명하지 않은 해 $x \neq 0$을 가진 필요충분조건은 행렬식이 0

                $D(\lambda) = \text{det} (A - \lambda I) = 0$

                    $= \begin{vmatrix} -5-\lambda & 2 \\ 2 & -2-\lambda \end{vmatrix} = (-5-\lambda)(-2-\lambda) - 2 \times 2$

                    $= \lambda^{2} + 7\lambda + 6 = 0$

                 $\lambda = \frac{-7 \pm \sqrt{7^{2} - 4 \times 1 \times 6}}{2 \times 1} = \frac{-7 \pm \sqrt{49 - 24}}{2}$

                 ∴ $\lambda_{1} = -1$,    $\lambda_{2} = -6$    ($A$의 고유값)

 

    b1) $\lambda_{1}$에 대응하는 $A$의 고유벡터

        식(2*),        $\lambda = \lambda_{1} = -1$

                $\left.\begin{matrix} -4x_{1} + 2x_{2} = 0 \\ 2x_{1} - x_{2} = 0 \end{matrix}\right\}    \Rightarrow    x_{2} = 2x_{1}$

                $\Rightarrow$ 이 식에서 $\lambda_{1} =-1$에 대응하는 $A$ 의 고유벡터가 상수배까지 결정

        만일 $x_{1} = 1$을 택하면 $x_{2} = 2$ 따라서 $\lambda = -1 $에 대응하는 의 고유벡터는

                $x_{1} = \begin{bmatrix} 1 \\ 2\end{bmatrix}$        $Ax = \lambda x$

        검증

                                       $A$         $x$           $\lambda x$

                $Ax_{1} = \begin{bmatrix} -5 & 2 \\ 2 & -2\end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} -1 \\ -2\end{bmatrix} = (-1)x_{1} = \lambda_{1} x_{1}$

 

    b2) $\lambda_{2}$에 대응하는 $A$의 고유벡터

                $\lambda = \lambda_{2} = -6$        식(2*)는

                $(-5-x)x_{1} - 2 x_{2} = 0$

                $2x_{1} + (-2-\lambda)x_{2} = 0$에 대입

                $\left.\begin{matrix} x_{1} + 2x_{2} = 0 \\ 2x_{1} + 4x_{2} = 0 \end{matrix}\right\}    \Rightarrow    x_{2} = -x_{1}/2$

        만일 $x_{1} = 2$를 택하면 $x_{2} = -1$

        $\lambda_{2} = -6$에 대응하는 $A$의 고유벡터는

                $x_{2} = \begin{bmatrix} -2 \\ -1 \end{bmatrix}$

 

    일반화

                $\begin{matrix} a_{11} x_{1} + a_{12} x_{2} + \cdots + a_{1n} x_{n} = \lambda x_{1} \\ a_{21} x_{1} + a_{22} x_{2} + \cdots + a_{2n} x_{n} = \lambda x_{2} \\ \vdots \\ a_{n1} x_{1} + a_{n2} x_{2} + \cdots + a_{nn} x_{n} = \lambda x_{n} \end{matrix}$

 

                $\begin{matrix} (a_{11} - \lambda) x_{1} + a_{12} x_{2} + \cdots + a_{1n} x_{n} = 0 \\ a_{21} x_{1} + (a_{22} - \lambda ) x_{2} + \cdots + a_{2n} x_{n} = 0 \\ \vdots \\ a_{n1} x_{1} + a_{n2} x_{2} + \cdots + (a_{nn} -\lambda) x_{n} = 0 \end{matrix}$

 

    행렬식 표현

                $(A-\lambda I) x = 0$

        Crammer  정리에서 $x \neq 0 \Rightarrow \text{det} A = 0$ (필요충분 조건)

                $D(\lambda) = \text{det}(A-\lambda I) = \begin{vmatrix} a_{11} - \lambda & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{21} - \lambda & \cdots & a_{2n} \\ \vdots &&& \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} - \lambda \end{vmatrix}$    특성방정식

                $D(\lambda)$ 전개 → $A$의 특성 방정식

 

정리 1 (고유값)

        정방행렬 $A$의 고유값은 $A$의 특성방정식의 근이다. 따라서, $n \times n$ 행렬은 적어도 하나 이상, 만아야 $n$개의 서로 다른 고유값을 갖는다.

 

정리 2 (고유벡터)

        만일 $x$가 행렬 $A$의 고유값 $\lambda$에 대응하는 고유벡터인 경우, 임의의 $k \neq 0$에 대하여 $kx$도 고유벡터가 된다.

        $Ax = \lambda x$

        $k(Ax) = A(kx) = \lambda(kx)$

 

○ 조립제법

        $x^{3} - 4x^{2} + 3x + 1 = (x-2) \square + \triangle$    ($\square $ : 몪,    $\triangle$ : 나머지)