행렬(Matrix) 3. 선형 연립방정식(2)

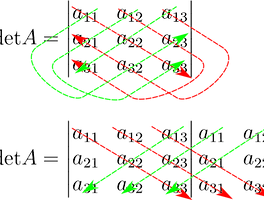
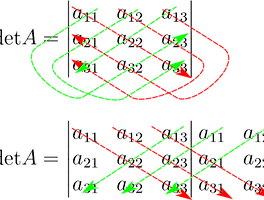
■ Gauss 소거법 : 연립 방정식의 세가지 경우

    1) 해를 무수해 많이 갖는 경우

        $\left[ \left. \begin{matrix} 3.0 & 2.0 & 2.0 & -5.0 & \\ 0.6 & 1.5 & 1.5 & -5.4 & \\ 1.2 & -0.3 & -0.3 & 2.4 & \\ \end{matrix}\right| \begin{matrix} 8.0 \\ 2.7 \\ 2.1 \end{matrix} \right ]$    $\Leftrightarrow$    $\begin{matrix} 3.0x_{1} + 2.0x_{2} + 2.0x_{3} - 5.0x_{4} = 8.0 \\ 0.6x_{1} + 1.5x_{2} + 1.5x_{3} - 5.4x_{4} = 2.7 \\ 1.2x_{1} - 0.3x_{2} - 0.3 x_{3} + 2.4x_{4} = 2.1 \end{matrix}$

    1 단계 : $x_{1}$ 을 소거(2번째, 3번째 방정식)

        $(-0.2)R_{1} + R_{2}, \; (0.4)R_{1} + R_{3}$

        $\left[ \left. \begin{matrix} 3.0 & 2.0 & 2.0 & -5.0 & \\ 0.0 & 1.1 & 1.1 & -4.4 & \\ 0.0 & -1.1 & -1.1 & 4.4 & \\ \end{matrix}\right| \begin{matrix} 8.0 \\ 1.1 \\ -1.1 \end{matrix} \right ]$ $\Leftrightarrow$ $\left. \begin{matrix} 3.0x_{1} + 2.0x_{2} + 2.0x_{3} - 5.0x_{4} = 8.0 \\ 1.2x_{2} + 1.1x_{3} - 4.4x_{4} = 1.1 \\ -1.1x_{2} - 1.1 x_{3} + 4.4x_{4} = -1.1 \end{matrix} \right.$

    2 단계 : $x_{2}$ 를 소거(3번째 방정식)

        $R_{2} + R_{3}$

        $\left[ \left. \begin{matrix} 3.0 & 2.0 & 2.0 & -5.0 & \\ 0.0 & 1.1 & 1.1 & -4.4 & \\ 0.0 & 0.0 & 0.0 & 0.0 & \\ \end{matrix}\right| \begin{matrix} 8.0 \\ 1.1 \\ 0 \end{matrix} \right ]$ $\Leftrightarrow$ $\begin{matrix} 3.0x_{1} + 2.0x_{2} + 2.0x_{3} - 5.0x_{4} = 8.0 \\ 1.1x_{2} + 1.1x_{3} - 4.4x_{4} = 1.1 \\ 0 = 0 \end{matrix}$

 

    후 치환

        2행 :  $x_{2} + x_{3} - 4x_{4} =1$    $\Rightarrow$    $x_{2} = 1 - x_{3} + 4x_{4}$ 

        1행 $x_{2}$ 대입

                $3x_{1} + 2(1-x_{3} + 4x_{4} ) + 2x_{3} - 5x_{4} = 8$

                $3x_{1} +2 - 2x_{3} + 8x_{4} + 2x_{3} - 5x_{4} = 8$

                $3x_{1} = 8 -2 -3x_{4}$

                $x_{1} = 2 - x_{4}$ ,               $x_{3}$, $x_{4}$ 는 임의로 결정가능 → 무한히 많은 해 존재

                $x_{3}$ , $x_{4}$ 의 값이 결정되면, $x_{1}$ , $x_{2}$ 의 값은 유일해

 

    2) 해가 존재하지 않는 경우

         $\left[ \left. \begin{matrix} 3 & 2 & 1 & \\ 2 & 1 & 1 & \\ 6 & 2 & 4 &\\ \end{matrix}\right| \begin{matrix} 3 \\ 0 \\ 6 \end{matrix} \right ]$ $\Leftrightarrow$ $\begin{matrix} 3x_{1} + 2x_{2} + x_{3} = 3 \\ 2x_{1} + x_{2} + x_{3} = 0 \\ 6x_{1} - 2x_{2} - 4x_{3} = 6 \end{matrix}$

   1 단계 : 2행, 3행의 $x_{1}$ 소거

         $(-2/3)R_{1} + R_{2}$ , $(-2)R_{1} + R_{3}$

         $\left[ \left. \begin{matrix} 3 & 2 & 1 & \\ 0 & -1/3 & 1/3 & \\ 0 & -2 & 2 &\\ \end{matrix}\right| \begin{matrix} 3 \\ -2 \\ 0 \end{matrix} \right ]$ $\Leftrightarrow$ $\begin{matrix} 3x_{1} + 2x_{2} + x_{3} = 3 \\ -1/3 x_{2} + 1/3 x_{3} = -2 \\ - 2x_{2} + 2x_{3} = 0 \end{matrix}$

    2 단계 : 3행 $x_{2}$ 소거

        $(-6)R_{2} + R_{3}$

        $\left[ \left. \begin{matrix} 3 & 2 & 1 & \\ 0 & -1/3 & 1/3 & \\ 0 & 0 & 0 &\\ \end{matrix}\right| \begin{matrix} 3 \\ -2 \\ 12 \end{matrix} \right ]$        $0 = 12$ $\Rightarrow$ 모순, 해가 존재하지 않음.

 

    3) 단일해를 갖는 경우